34. PyTorch 中的卷积层
PyTorch 中的卷积层
要在 PyTorch 中创建卷积层,必须首先导入必要的模块:
import torch.nn as nn然后定义卷积层和模型的前馈行为(输入如何经过网络层级)。首先必须定义一个 Model 类并填写两个函数。
init
你可以通过以下格式在 __init__ 函数里定义卷积层:
self.conv1 = nn.Conv2d(in_channels, out_channels, kernel_size, stride=1, padding=0)forward
然后在 forward 函数里引用该层级!在此例中,我传入了输入图像 x,并向此层的输出应用了 ReLU 函数。
x = F.relu(self.conv1(x))参数
必须传递以下参数:
in_channels- 输入数量(深度),例如 RGB 图像是 3。out_channels- 输出通道的数量,即卷积层包含的过滤“图像”数量,或者将应用到输入上的唯一卷积核数量。kernel_size- 表示(方形)卷积核的高度和宽度。
你还可以调整其他可选参数:
stride- 卷积步长。如果不指定任何值,stride将设为1。padding- 输入数组周围的 0 边。如果不指定任何值,padding将设为0。
注意:可以将 kernel_size 和 stride 表示为数字或元组。
你还可以设置很多其他可调参数,从而更改卷积层的行为。要了解详情,请参阅此官方文档。
池化层
池化层的参数是核大小和步长。通常和下采样因子的值一样。例如,以下代码将使输入的 x-y 维度下采样到一半大小:
self.pool = nn.MaxPool2d(2,2)forward
以下代码将池化层应用到了 forward 函数。
x = F.relu(self.conv1(x))
x = self.pool(x)卷积示例 1
假设我要构建一个 CNN,输入层接受的是 200 x 200 像素(对应于高 200、宽 200、深 1 的三维数组)的灰阶图像。然后,假设下一层是一个卷积层,包含 16 个过滤器,每个过滤器的宽和高都是 2。在进行卷积运算时,我希望过滤器一次跳过 2 个像素。但是我不希望过滤器越过图像边界;换句话说,我不想用 0 填充图像。要构建此卷积层,我会使用以下代码:
self.conv1 = nn.Conv2d(1, 16, 2, stride=2)卷积示例 2
假设我希望下一层是一个卷积层,它将在示例 1 中构建的层级作为输入。假设新层级有 32 个过滤器,每个的高和宽是 3。在进行卷积运算时,我希望过滤器一次跳过 1 个像素。为了使此层的宽和高与输入层的一样,我将填充图像。要构建此卷积层,我会使用以下代码:
self.conv2 = nn.Conv2d(16, 32, 3, padding=1)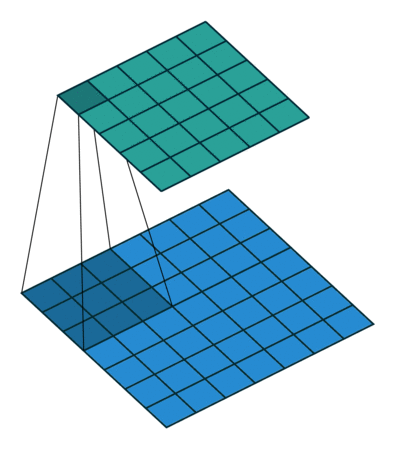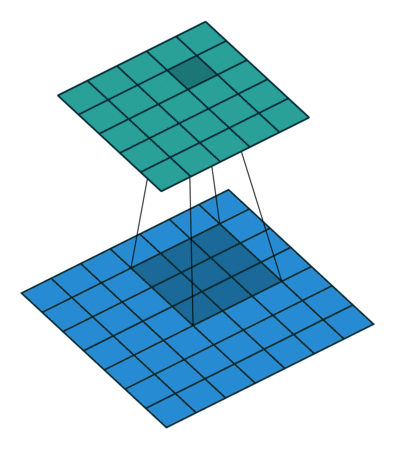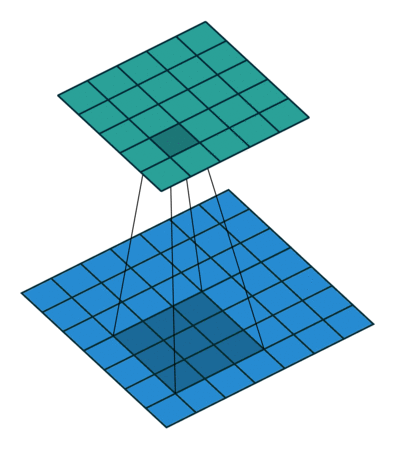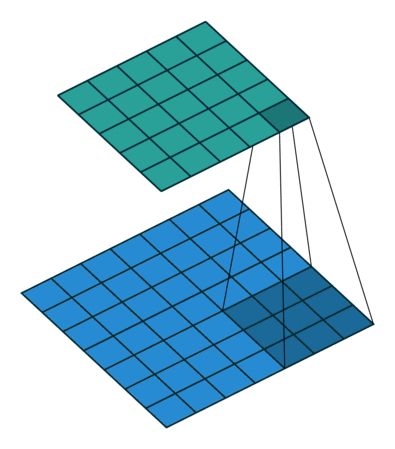
用 3x3 窗口和步长 1 进行卷积运算
图像来源:http://iamaaditya.github.io/2016/03/one-by-one-convolution/
序列模型
我们还可以在 __init__ 函数里使用 Sequential 封装容器,这样就能在 PyTorch 中创建 CNN 模型。序列模型使我们能够堆叠不同的层级,并在层级之间指定激活函数。
def __init__(self):
super(ModelName, self).__init__()
self.features = nn.Sequential(
nn.Conv2d(1, 16, 2, stride=2),
nn.MaxPool2d(2, 2),
nn.ReLU(True),
nn.Conv2d(16, 32, 3, padding=1),
nn.MaxPool2d(2, 2),
nn.ReLU(True)
)公式:卷积层中的参数数量
卷积层中的参数数量取决于为 filters/out_channels、kernel_size 和 input_shape 设定的值。需要定义以下变量:
K- 卷积层中的过滤器数量F- 卷积过滤器的高和宽D_in- 上一层的深度
注意 K = out_channels,以及 F = kernel_size。同样,D_in 是 input_shape 元组中的最后一个值,通常是 1 或 3(分别表示 RGB 和灰阶图像)。
因为每个过滤器有 F*F*D_in 个权重,并且卷积层由 K 个过滤器组成,所以卷积层中的权重总数是 K*F*F*D_in。由于每个过滤器有一个偏差项,所以卷积层有 K 个偏差。卷积层的参数数量是 K*F*F*D_in + K。
公式:卷积层的形状
卷积层的形状取决于为 kernel_size、input_shape、padding 和 stride 设定的值。需要定义以下变量:
K- 卷积层中的过滤器数量F- 卷积过滤器的高和宽S- 卷积步长P- 填充W_in- 上一层的宽/高(方形)
注意 K = out_channels、F = kernel_size 以及 S = stride。同样,W_in 是 input_shape 元组的第一个和第二个值。
卷积层的深度将始终等于过滤器数量 K。
卷积层的空间维度计算公式为:
(W_in−F+2P)/S+1
扁平化
要完成 CNN 结构,有一个步骤是扁平化一系列卷积层和池化层的最终输出,这样才能作为向量参数输入线性分类层中。在此步骤,你必须知道层级输出的确切参数数量。
下面做道练习,假设输入图像的深度是 130x130 (x, y) and 3 (RGB)。该图像按顺序经过了以下层级:
nn.Conv2d(3, 10, 3)
nn.MaxPool2d(4, 4)
nn.Conv2d(10, 20, 5, padding=2)
nn.MaxPool2d(2, 2)